Which Of The Following Changes Would Improve The Accuracy Of The Molar Mass Measurement

Colligative Properties and Conclusion of Molar Mass

Table of contents

Colligative Properties and Determination of Molar Mass Relative Lowering of Vapour Force per unit area Summit of Boiling Indicate Depression of Freezing Point Osmosis and Osmotic Pressure Applications of Osmosis

Colligative Properties and Determination of Molar Mass

When we a non-volatile solute in a volatile solvent we notice that at that place is a decrease in vapour pressure of the solution. This decrease of vapour pressure can be quantitatively used to measure several properties of liquid solutions.These backdrop depend more on solute particles of the solution and are called colligative backdrop. The word "colligative" is derived from the Latin discussion "coligare" which means "to bind together". The post-obit properties come in the category of colligative backdrop.

• Relative Lowering of Vapour Pressure

• Pinnacle of Boiling Point

• Depression of Freezing Point

• Osmosis and Osmotic Force per unit area
  

Relative Lowering of Vapour Pressure

Image ane: There is a relative lowering of vapour pressure considering less surface area is available for the solvent molecules to escape out.

The vapour force per unit area of a solvent is lowered when we add a non-volatile solute in it; this is called Lowering of Vapour Pressure. The French chemist François-Marie Raoult's observed that the concentration of solute particles is mainly responsible for the lowering of vapour pressure level and too discovered a relation between vapour force per unit area of solution, vapour pressure level of pure solvent and mole fraction of solute and solvent.

Image 2: The vapour pressure decreases as nosotros add together solute in pure solvent

If the vapour pressure of the solution is P₁, the vapour pressure of the pure solvent is P_i ⁰ and mole fraction of solvent is ten₁, and so according to Raoult's Law:

P₁ = P_ane ⁰ 10_one

The decrement in vapour pressure level of solvent that is, Δ P₁ will exist

Decrement in Vapour Pressure = Vapour Pressure level of Pure Solvent – Vapour Pressure level of Solvent

Δ P₁ = P₁ ⁰ – P₁

Substituting P₁ = P₁ ⁰ x_ane in the higher up relation we become,

Δ P₁ = P₁ ⁰ –  P₁ ⁰ 10_one

Δ P_i = P₁ ⁰ (1 – ten₁)

Since the sum of mole fraction of solute ( x_ii) and mole fraction of solvent ( x_i) is 1, we tin can write

1 – x₁ = x₂

Δ P₁ = P_ane ⁰ ten₂

It is obvious that subtract in vapour pressure depends on mole fraction of solute (x₂) as mentioned by Raoult's.

The equation tin can be re-written equally:

The term is called Relative Lowering in vapour pressure and equals to mole-fraction of the solute.

If n₁ and n₂ are the respective moles of solute and solvent, and then we can re-write the equation equally:

If the solution is quite diluted, we can neglect moles of solute north_one in front of moles of solvent n₂. So, in instance of dilute solution, the equation becomes

We know that moles of any substance can exist calculated by dividing the given mass past its molecular mass. Then moles of solute (n₂) is equal to

where m₂ and One thousand₂ are given mass and molecular mass of solute.

Similarly, a mole of solvent (n_one) equals

Substituting the value of n_ane and north₂ in the dilute solution vapour pressure relation, nosotros get

And then, we know the other quantities, we can easily determine the molar mass of solute M₂ with the in a higher place relation.

Example: The vapour pressure level of pure benzene is 0.850 confined at room temperature. On addition of 0.half dozen g of non-volute solute in 39 grand of benzene solution, the vapour pressure level of benzene reduces to 0.845 bars. What is the tooth mass of solute?

Nosotros take

P₁ ⁰ = 0.850 bar, P_one = 0.845 bar, m_ane = 39 g, M_one = 78 g and m_ii = 0.6 thousand. Now the unknown quantity is M₂ which is the molar mass of non-volatile solute.

Using the relative lowering of vapour pressure relation, we get:

The change in vapour pressure Δ P₁ = P₁ ⁰ – P₁, equals to 0.850 – 0.845 = 0.05 bar. Substituting the respective values in the relation we get

Computing, we become the value of Grand_two as xx.68 one thousand.

Image 2: There is a relative lowering of vapour pressure because less surface expanse is available for the solvent molecules to escape out.

Superlative of Boiling Signal

Nosotros know that on addition of non-volatile solute in a solvent, the vapour pressure of the solvent decreases. Nevertheless the humid point of the solution is greater than that of the pure solvent, this is because vapour pressure is directly proportional to temperature. And in gild to boil a solution, we need to enhance the humid indicate of the solution to a certain temperature. This raising of temperature is called elevation of boiling point and just like the relative lowering of vapour force per unit area it also depends on solute particles in the solution.

Mathematically, if T_b ⁰ is the boiling point of pure solvent and T_b denotes boiling point of the solution, then elevation in humid point (denoted by Δ T_b) is

Δ T_b = T_b – T_b ⁰

Experimentally it has been found that pinnacle in boiling point in dilute solutions is directly proportional to molality 'm' of solute nowadays in a solution.

Δ T_b ∝ one thousand

Δ T_b = 1000_b thou

The term molality 'grand' denotes the number of moles of solute present in thousand one thousand or ane kg of solvent. In the relation K_b is the chosen molal superlative constant or ebullioscopic constant. The standard unit of measurement of molal acme abiding K_b is K kg mol^-1.

Allow thou₁ and yard₂ exist the given masses of solvent and solute respectively. And tooth masses of solute exist M₂ and that of solvent is M_ane, then molality can be evaluated from the relation:

Putting the value of molality in the boiling tiptop relation, we get

Hence, if know the remaining quantities nosotros can easily determine the molar mass of solute with the humid elevation relation.

Example: The boiling signal of a pure liquid is 353.23 Thou. If we add 2.70 1000 of a non-volatile solute in ninety yard of liquid, the boiling point of the solution rises to 354.eleven G. What will exist the molar mass of non-volatile solute? Take the value of 1000_b of liquid to be 2.53 K kg mol^-1.

So we have

T_b ⁰ = 353.23 One thousand, T_b = 354.11 1000, m_two = 2.seventy thousand, K_b = 2.53 G kg mol^-1 and m_ane = 90 1000.

The elevation in humid point Δ T_b = T_b – T_b ⁰ = 354.11K – 353.23K =0.88

 Using the above relation we get:

Calculating by we go the value of K₂ to be 86.25 grand, hence molar of the mass of solute is 86.25 thou.

Depression of Freezing Bespeak

When the vapour pressure of a solution is reduced, the freezing of the solution decreases. The freezing signal of a solution is divers every bit the temperature at which vapour pressure of its substance go equal in liquid and vapour phase. If the vapour pressure of the solution equals to vapour pressure level of the pure solvent, and so the solution will be frozen. Co-ordinate to Raoult's Law when we add together a non-volatile solute in a solvent we find that the freezing point of the solution is slightly less than that of the pure solvent. This is called depression of freezing point.

The freezing point depression is denoted by Δ T_f and equals to

Δ T_f = T_f ⁰ - T_f

The freezing point depression for dilute solutions is straight proportional to molality of the solute, but like the boiling elevation bespeak. That is

Δ T_f ∝ grand

Δ T_f = K_f m

The proportionality constant K_f is chosen Molal Low Abiding and is too known as Cryoscopic Constant, which depends upon the nature of the solvent.

We know that molality 'm' equals to

where m_two is a mass of solute, m₁ is a mass of solvent and M_two is the tooth mass of added non-volatile solute.

Putting the value of molality in to a higher place equation nosotros get low in freezing point equally

Hence, nosotros can utilize depression of freezing point to evaluate tooth mass of solute.

Prototype 3: A brain map to think how to calculate the tooth mass of solute when depression in freezing point is given.

The table below depicts boiling and freezing points of important solvents with their molal constants.

Solvent	Boiling Point (Thousand)	Kb ( Thou kg mol-1)	Freezing Point     (Thousand)	Kf ( Yard kg  ol-ane)
H2o	373.xv	0.52	273	1.86
Ethanol	351.5	1.20	155.7	1.99
Cyclohexane	353.74	2.79	279.55	20
Benzene	353.three	2.53	278.6	5.12
Chloroform	334.4	iii.63	209.6	4.79
Acetic Acrid	391.1	2.93	290	3.90
Diethyl Ether	307.8	2.02	156.9	1.79

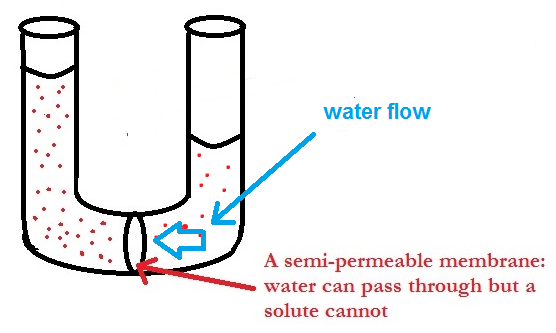
Osmosis and Osmotic Force per unit area

Image 4: Osmosis process

Osmosis is defined every bit the flow of liquid through a semi-permeable membrane which allows only solvent molecules to pass through it. The term membrane tin be well-understood from existent life examples like claret cells get destroyed when placed in a common salt-h2o solution, raw mangoes get shrined when we gear up pickles with alkali solution etc. A membrane is a continuous sheet or film with a pore network embedded in such way that information technology allows just desired substances to menstruation through it. It can be natural like a sus scrofa'south float or it can exist human being-made as cellophane is.

The membrane which allows merely minor solvent molecules to pass through information technology and resist the menstruum of bigger solute molecules is called Semipermeable Membrane or SPM.

Osmotic Pressure is the defined as the actress pressure 1 can add together to terminate the solvent molecules to flow. In other words, the force per unit area exerted on a solution to forestall osmosis with the help of semi-permeable membrane is called Osmotic Force per unit area. Osmotic pressure is a colligative property and depends on solute particles of the solution. Experimentally for dilute solutions, osmotic pressure is

π = CRT

where π is osmotic pressure, R is gas constant, T is abiding and C denotes concentration or molarity of the solution.

Molarity (C) is defined equally moles of solute divided past the volume of solution in liters. Mathematically

C = due north₂ / V

where n₂ is moles of solute and V is the book of the solution. Putting the value of c in osmotic pressure we get

π = (n_ii / V) R T

Since moles north₂ = m_two /M₂, where thousand_two is given mass and M₂ is molar mass, nosotros can derive a new relation between osmotic pressure and molar mass of solute One thousand₂ every bit

Thus, if nosotros know the remaining quantities we can easily make up one's mind the molecular masses of solute. In fact, this method is used to determine molecular masses of several biomolecules, proteins, and polymers. The advantage of using osmotic pressure level is that we utilize molarity of the solution instead of molality at standard room temperature.

We can likewise make up one's mind density of the solution with the relation

π = d thou h

where π is osmotic pressure, d is density of the solution, g is acceleration due to gravity and h is tiptop of the liquid column.

Paradigm 5: Relation between osmotic pressure and density of the solution

Notes:

• Two solutions which accept same osmotic pressure level are said to be isotonic solutions and when we separate these solutions by an SPM, osmosis never occurs

• The solution with higher osmotic pressure as compared to other solution is called Hypertonic Solution

• The solution with lower osmotic pressure as compared to other solution is chosen Hypotonic Solution

Applications of Osmosis

Osmosis procedure is of great utility in commercial and daily life. Information technology has following applications:

• Contrary Osmosis, (a procedure in which nosotros reverse the management of osmosis by applying larger pressure than osmotic pressure on the other side, which aid in getting pure solvent out of the solution) is used to obtain fresh water from the bounding main h2o

Epitome six: We add cellulose acetate to human action equally semipermeable membrane

• Also, we utilize cellulose acetate membrane to obtain fresh water as information technology merely allows pure water solvent molecules and is impermeable to impurities and ions nowadays in contaminated h2o

Watch this Video for more than reference

More Readings

Colligative Properties and Determination of Tooth Mass

Source: https://www.askiitians.com/iit-jee-solutions-colligative-properties/colligative-properties-and-determination-of-molar-mass/

Posted by: williscappiket.blogspot.com

Share this post